class: center, middle, inverse, title-slide # Regional disparities and heterogeneous convergence in Indonesia ### Carlos Mendez<br /><a href="https://carlos-mendez.org" class="uri">https://carlos-mendez.org</a><br /><br />Associate Professor<br />Graduate School of International Development<br />Nagoya University<br /> JAPAN ### May 28th, 2021 <br /><br />[ Slides available at: <a href="https://quarcs-lab.org" class="uri">https://quarcs-lab.org</a> ] --- class: center, middle <style type="text/css"> .highlight-last-item > ul > li, .highlight-last-item > ol > li { opacity: 0.5; } .highlight-last-item > ul > li:last-of-type, .highlight-last-item > ol > li:last-of-type { opacity: 1; } </style> # A summary of the paper in 2 slides... --- class: highlight-last-item ## Motivation: - Large regional disparities in Indonesia and **an east-west divide** -- - Previous convergence studies largely **ignored the role of spatial heterogeneity and scale** -- ## Research Objective: - (Re)evaluate the regional convergence hypothesis across districts of Indonesia with particular **emphasis on spatial heterogeneity and scale** -- ## Methods: - Simple (non-spatial) **beta-convergence** model -- - Geographically weighted regression (**GWR**) beta-convergence model -- - Multiscale geographically weighted regression (**MGWR**) beta convergence model -- ## Data: - GDP per capita, years of schooling, public investment -- - **514** Indonesian districts over the **2010-2018 period** -- --- class: middle, highlight-last-item ## Main Results: 1. Regional convergence is a **heterogeneous and multiscale** process -- 2. East-west divide: Significant **convergence only in the west** -- 3. Significant heterogeneity and scale effects in the **determinants of regional growth** --- class: middle # Outline of this presentation 1. Some stylized facts - Large regional disparities - An east-west divide - On average, poor regions are catching up 2. Heterogeneous and multiscale convergence model - A Simple beta-convergence model - Add heterogeneity: The GWR beta-convergence model - Add scale: The MGWR beta-convergence model 3. Main results of the paper - Regional convergence is a heterogeneous and multiscale process - East-west divide: Significant convergence only in the west - Significant heterogeneity and scale effects in the determinants of regional growth [ Slides available at: https://quarcs-lab.org] --- class: center, middle # (1) Some stylized facts --- class: middle,center ## Large regional disparities 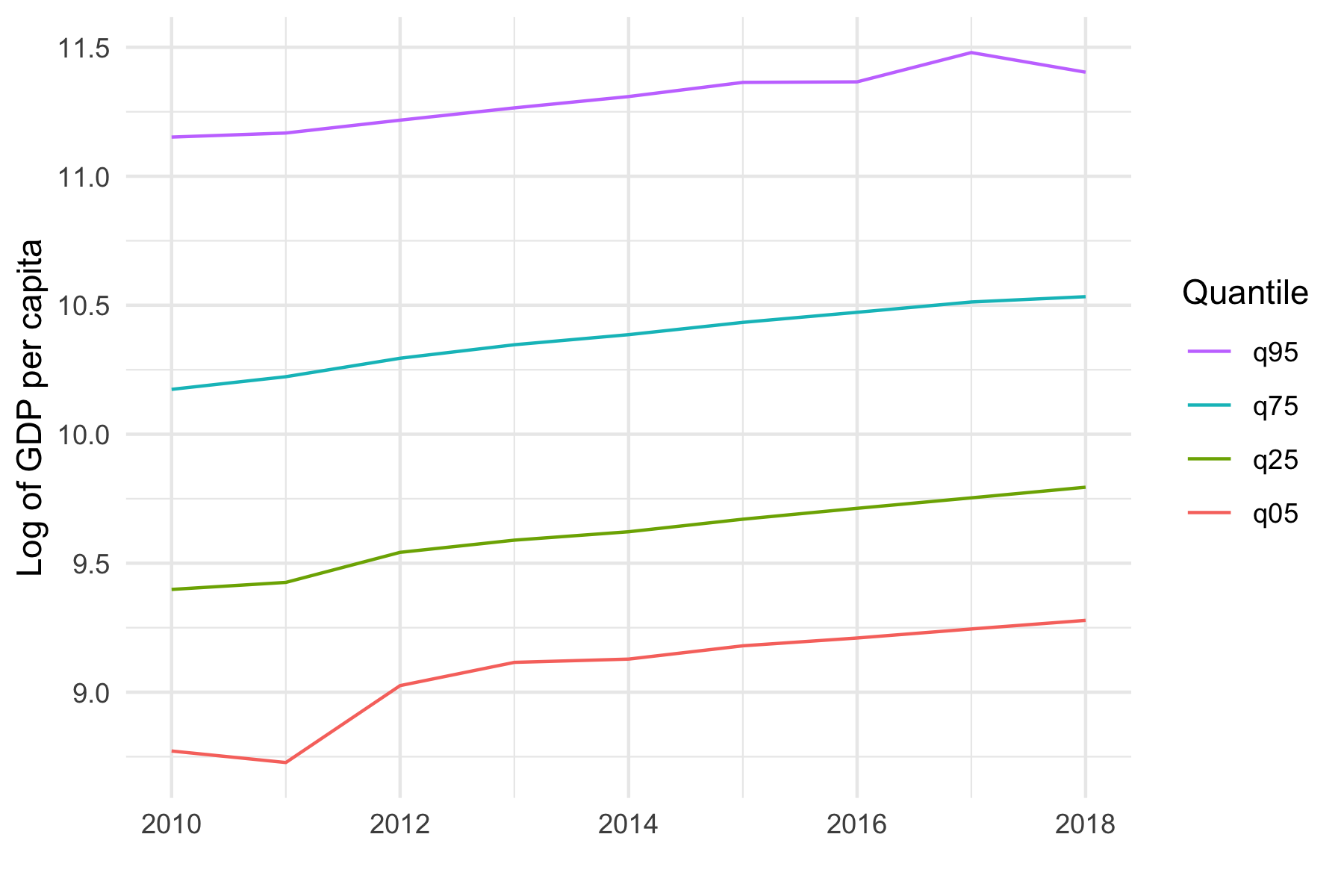 --- class: middle,center ## An east-west regional divide 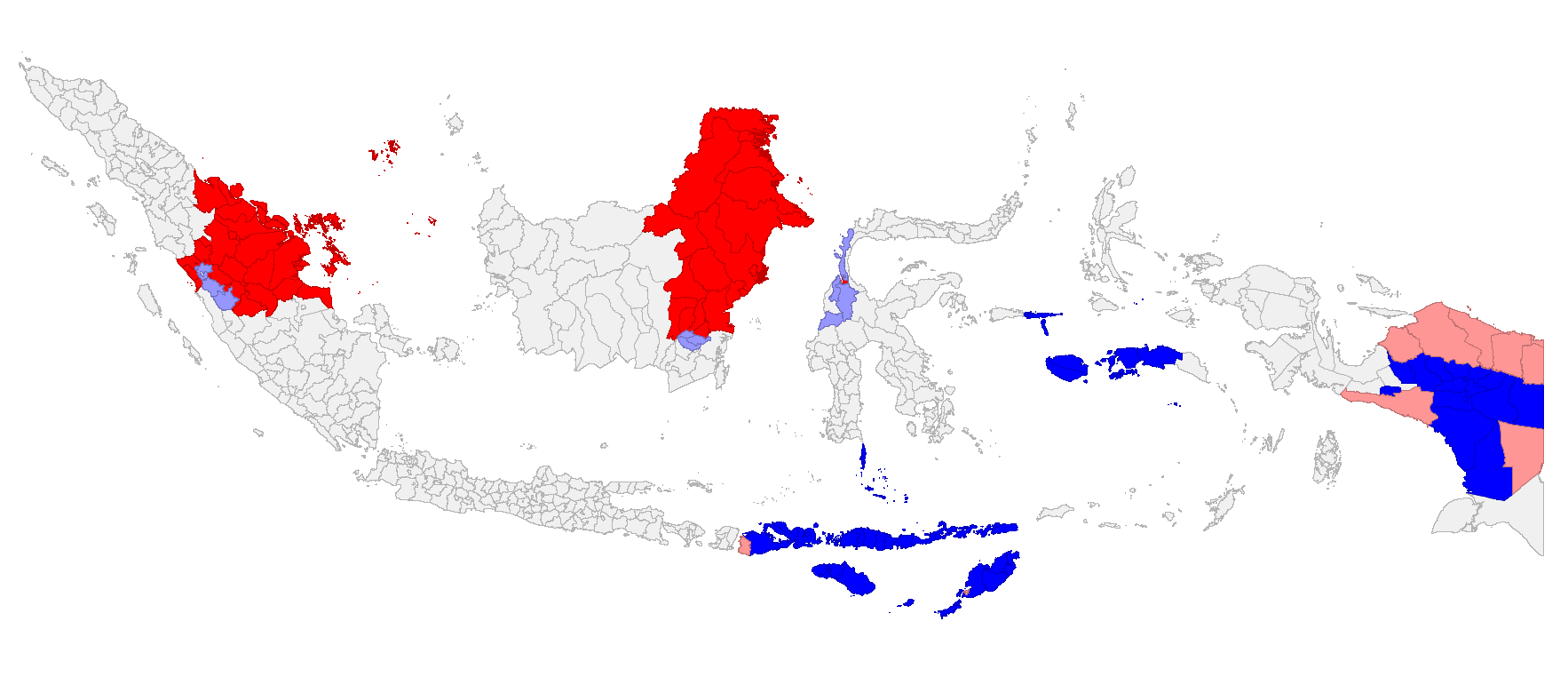 Hot spots and cold spots of Log GDP per capita in 2018 --- class: middle,center ## On average, poor regions are catching up 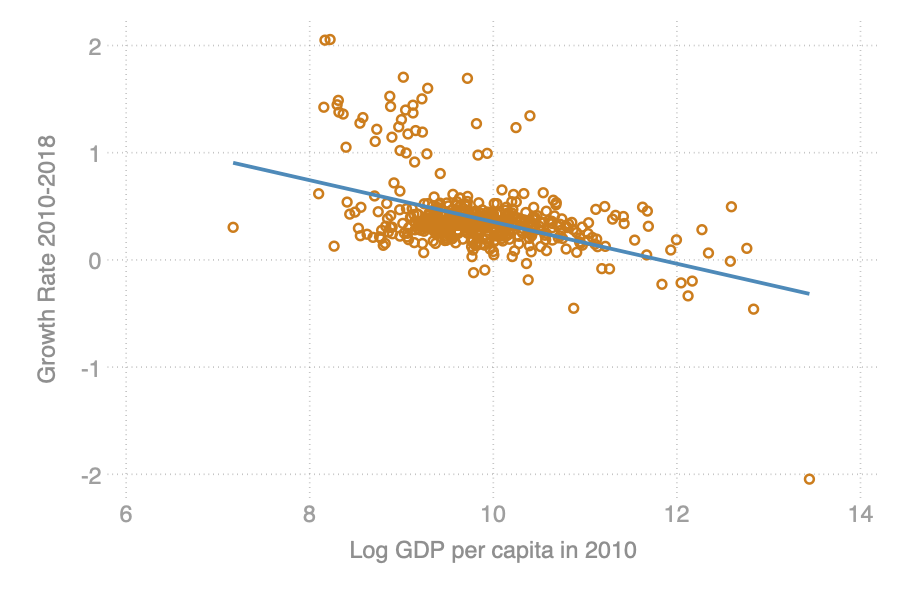 --- class: center, middle # (2) Heteregeneous and multiscale convergence framework --- class: middle ## Start with a simple (non-spatial) beta-convergence model 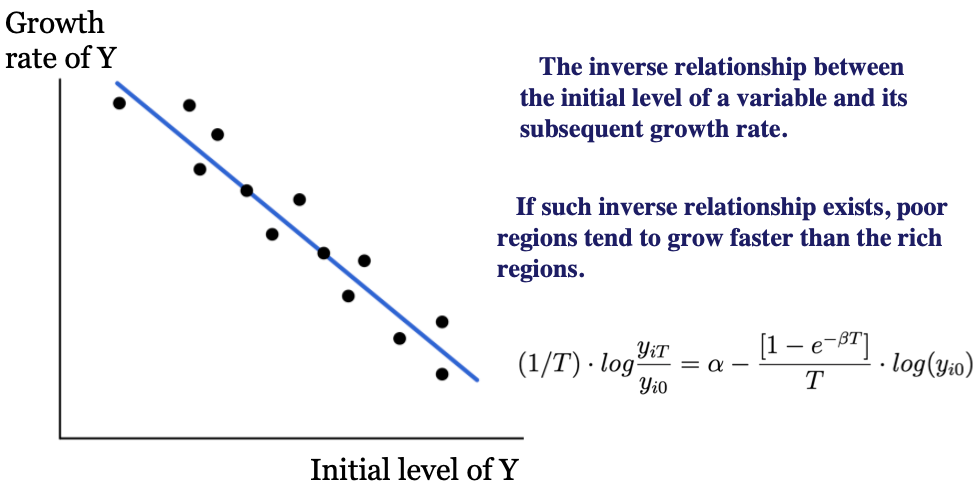 `$$g(y_i)_{0,T} = \beta_0 - \beta_1log(y_i)_0 + \sum_{j=1}^{k} \beta_{j}\left(x_{ji} \right)_0 + \epsilon_i$$` We can study an effect's direction and magnitude --- class: middle ## Add spatial heterogeneity via the GWR model 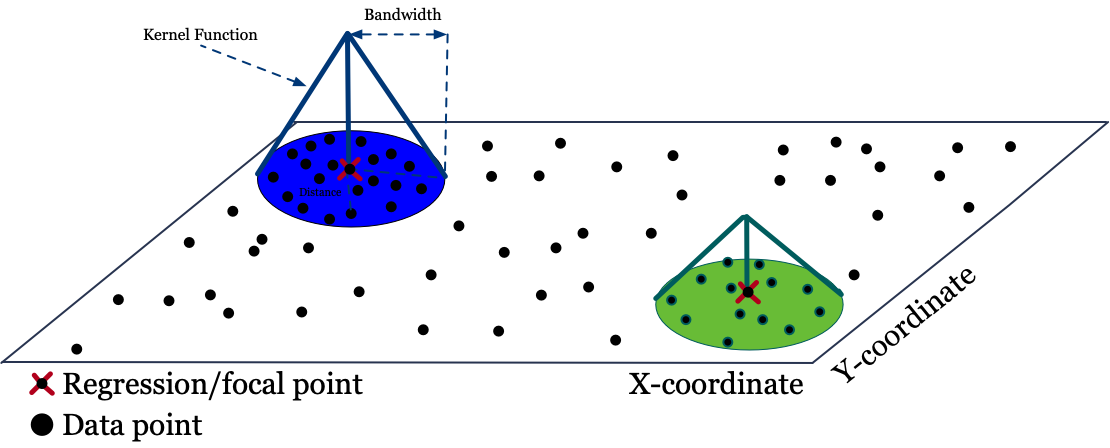 `$$g(y_i)_{0,T} = \beta_{0i\left(Y_{i}, X_{i}\right)} - \beta_{1i\left(Y_{i}, X_{i}\right)} log(y_i)_0 + \sum_{j=1}^{k} \beta_{ji\left(Y_{i}, X_{i}\right)} \left(x_{ji} \right)_0 + \epsilon_i$$` We can study an effect's direction, magnitude, and **location** --- class: middle ## Add spatial heterogeneity and scale via the MGWR model  `$$g(y_i)_{0,T} = \beta_{0i\left(Y_{i}, X_{i}\right)}^{BW(0)} - \beta_{1i\left(Y_{i}, X_{i}\right)}^{BW(1)} log(y_i)_0 + \sum_{j=1}^{k} \beta_{ji\left(Y_{i}, X_{i}\right)}^{BW(j)} \left(x_{ji} \right)_0 + \epsilon_i$$` We can study an effect's direction, magnitude, **location**, and **scale** --- class: middle, center # (3) Main results --- class: middle, center ## Regional convergence is a heterogeneous process 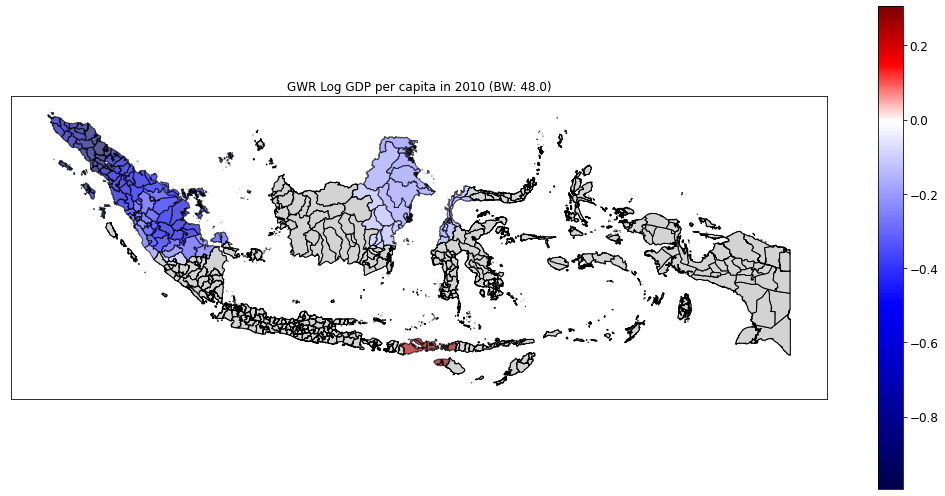 GWR beta-convergence approach Understand an effect's direction, magnitude, and **location** --- class: middle, center ## Regional convergence is a heterogeneous and multiscale process 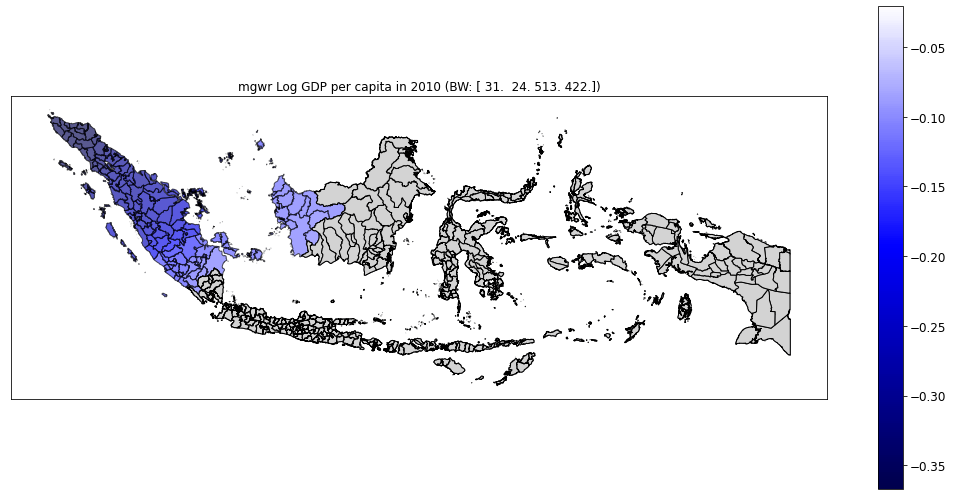 MGWR beta-convergence approach Understand an effect's direction, magnitude, **location**, and **scale** --- class: middle, center ## Revisiting the east-west divide: Only the west is converging  MGWR beta-convergence approach --- class: middle, center ## Heterogeneity in schooling effects: GWR vs MGWR Statistically significant heterogeneity when using GWR  GWR approach --- class: middle, center ## Heterogeneity and scale in schooling effects No statistically significant heterogeneity when using MGWR  MGWR approach --- class: middle, center ## Heterogeneity in public investment effects: GWR vs MGWR Positive and negative effects of public investment when using GWR 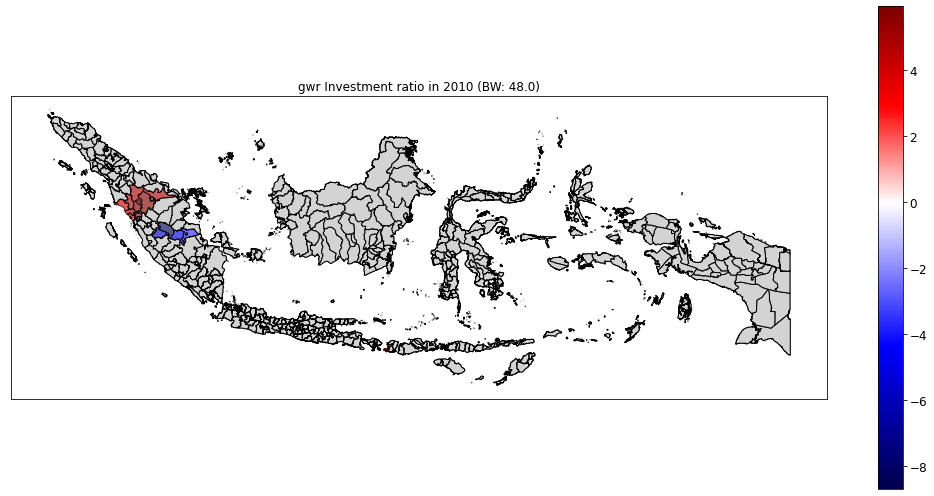 GWR approach --- class: middle, center ## Heterogeneity and scale in public investment effects Mostly positive effects of public investment when using MGWR Again, a clear east-west divide 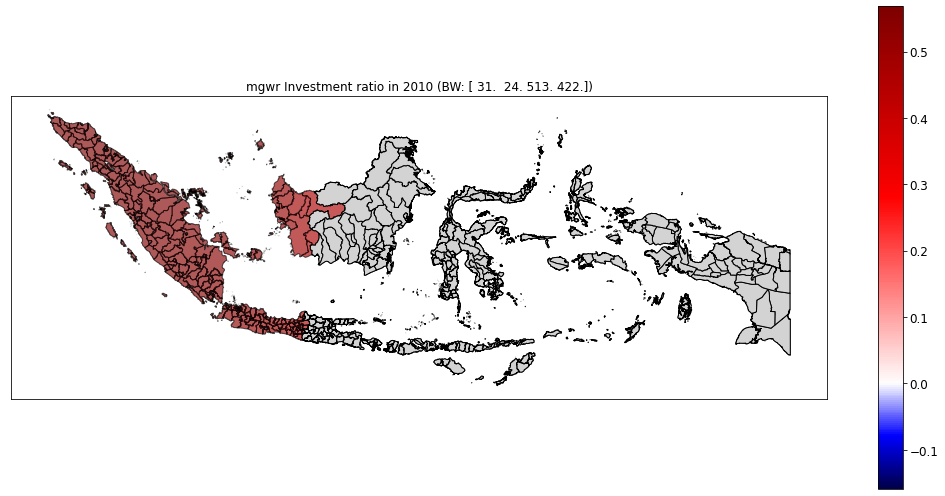 MGWR approach --- class: highlight-last-item # Concluding Remarks ## Main results - Regional convergence is both **heterogeneous and multiscale** -- - On the east-west divide: Significant convergence **only in the west** -- - Heterogeneity and scale effects in the **determinants** of regional growth -- ## Implications and further research Heterogeneity and scale can **enrich** the simple beta-convergence framework -- - Identify location-specific convergence speeds -- - Study the geographical scale of the convergence process -- - Identify location-specific determinants of growth -- - Study scale effects in the determinants of growth -- **Next steps:** (1) Add structural change variables, (2) evaluate interactions with the convergence speed, (3) compare with semiparametric-GWR models, (4) evaluate residual spatial dependence. --- class: center, middle # Thank you for your attention https://carlos-mendez.org Slides available at: https://quarcs-lab.org  **Quantitative Regional and Computational Science lab** https://quarcs-lab.org *** This research project was supported by JSPS KAKENHI Grant Number 19K13669 --- # Selected references - Aginta, H., Gunawan, A. B., & Mendez, C. (2021). Regional Income Disparities and Convergence Clubs in Indonesia: New District-Level Evidence 2000-2017. Journal of the Asia Pacific Economy, Forthcoming. https://doi.org/10.1080/13547860.2020.1868107 - Brunsdon, C., Fotheringham, A. S., & Charlton, M. E. (1996). Geographically weighted regression: A method for exploring spatial nonstationarity. Geographical Analysis, 28(4), 281–298. - Eckey, H.-F., Kosfeld, R., & Türck, M. (2007). Regional convergence in Germany: A geographically weighted regression approach. Spatial Economic Analysis, 2(1), 45–64. https://doi.org/10.1080/17421770701251905 - Fotheringham, A. S., Yang, W., & Kang, W. (2017). Multiscale Geographically Weighted Regression (MGWR). Annals of the American Association of Geographers, 107(6), 1247–1265. https://doi.org/10.1080/24694452.2017.1352480 - Yu, H., Fotheringham, A. S., Li, Z., Oshan, T., Kang, W., & Wolf, L. J. (2020). Inference in Multiscale Geographically Weighted Regression. Geographical Analysis, 52(1), 87–106. https://doi.org/10.1111/gean.12189